2023 MAA AMC 10A
- Cities \( A \) and \( B \) are 45 miles apart. Alicia lives in \( A \) and Beth lives in \( B \) . Alicia bikes towards \( B \) at 18 miles per hour. Leaving at the same time, Beth bikes toward \( A \) at 12 miles per hour. How many miles from City \( A \) will they be when they meet?
- The weight of \( \frac{1}{3} \) of a large pizza together with \( 3\frac{1}{2} \) cups of orange slices is the same as the weight of \( \frac{3}{4} \) of a large pizza together with \( \frac{1}{2} \) cup of orange slices. A cup of orange slices weighs \( \frac{1}{4} \) of a pound. What is the weight, in pounds, of a large pizza?
- How many positive perfect squares less than 2023 are divisible by 5 ? 在小于 2023 的正的完全平方数中, 有多少个数可以被 5 整除?
- A quadrilateral has all integer side lengths, a perimeter of 26 , and one side of length 4 . What is the greatest possible length of one side of this quadrilateral?
- How many digits are in the base-ten representation of \( {8}^{5} \cdot {5}^{10} \cdot {15}^{5} \) ? \( {8}^{5} \cdot {5}^{10} \cdot {15}^{5} \) 的十进制表示中有多少个数字?
- An integer is assigned to each vertex of a cube. The value of an edge is defined to be the sum of the values of the two vertices it touches, and the value of a face is defined to be the sum of the values of the four edges surrounding it. The value of the cube is defined as the sum of the values of its six faces. Suppose the sum of the integers assigned to the vertices is 21 . What is the value of the cube?
- Janet rolls a standard 6-sided die 4 times and keeps a running total of the numbers she rolls. What is the probability that at some point, her running total will equal 3 ?
- Barb the baker has developed a new temperature scale for her bakery called the Breadus scale, which is a linear function of the Fahrenheit scale. Bread rises at 110 degrees Fahrenheit, which is 0 degrees on the Breadus scale. Bread is baked at 350 degrees Fahrenheit, which is 100 degrees on the Breadus scale. Bread is done when its internal temperature is 200 degrees Fahrenheit. What is this in degrees on the Breadus scale?
- A digital display shows the current date as an 8-digit integer consisting of a 4-digit year, followed by a 2-digit month, followed by a 2-digit date within the month. For example, Arbor Day this year is displayed as 20230428. For how many dates in 2023 does each digit appear an even number of times in the 8-digit display for that date?
- Maureen is keeping track of the mean of her quiz scores this semester. If Maureen scores an 11 on the next quiz, her mean will increase by 1 . If she scores an 11 on each of the next three quizzes, her mean will increase by 2 . What is the mean of her quiz scores currently?
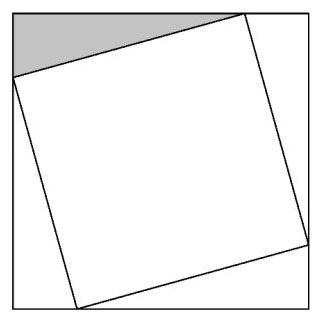
- A square of area 2 is inscribed in a square of area 3 , creating four congruent triangles, as shown below. What is the ratio of the shorter leg to the longer leg in the shaded right triangle?
- How many three-digit positive integers \( N \) satisfy the following properties?
- The number \( N \) is divisible by 7 .
- The number formed by reversing the digits of \( N \) is divisible by 5 .
- 数 \( N \) 可以被 7 整除.
- 将组成 \( N \) 的数字顺序反转后所得的数能被 5 整除.
- Abdul and Chiang are standing 48 feet apart in a field. Bharat is standing in the same field as far from Abdul as possible so that the angle formed by his lines of sight to Abdul and Chiang measures \( {60}^{ \circ } \) . What is the square of the distance (in feet) between Abdul and Bharat?
- A number is chosen at random from among the first 100 positive integers, and a positive integer divisor of that number is then chosen at random. What is the probability that the chosen divisor is divisible by 11 ?
- An even number of circles are nested, starting with a radius of 1 and increasing by 1 each time, all sharing a common point. The region between every other circle is shaded, starting with the region inside the circle of radius 2 but outside the circle of radius 1 . An example showing 8 circles is displayed below. What is the least number of circles needed to make the total shaded area at least \( {2023\pi } \) ?
- In a table tennis tournament every participant played every other participant exactly once. Although there were twice as many right-handed players as left-handed players, the number of games won by left-handed players was 40% more than the number of games won by right-handed players. (There were no ties and no ambidextrous players.) What is the total number of games played?
- Let \( {ABCD} \) be a rectangle with \( {AB} = {30} \) and \( {BC} = {28} \) . Points \( P \) and \( Q \) lie on \( \overline{BC} \) and \( \overline{CD} \) , respectively, so that all sides of \( \bigtriangleup {ABP},\bigtriangleup {PCQ} \) , and \( \bigtriangleup {QDA} \) have integer lengths. What is the perimeter of \( \bigtriangleup {APQ} \) ?
- A rhombic dodecahedron is a convex polyhedron where each of the 12 faces is a rhombus, and all of the faces are congruent to each other. The number of edges that meet at a vertex is either 3 or 4 , depending on the vertex. What is the number of vertices at which exactly 3 edges meet?
- The line segment from \( A\left( {1,2}\right) \) to \( B\left( {3,3}\right) \) can be transformed to the line segment from \( {A}^{\prime }\left( {3,1}\right) \) to \( {B}^{\prime }\left( {4,3}\right) \) , sending \( A \) to \( {A}^{\prime } \) and \( B \) to \( {B}^{\prime } \) , by a rotation centered at the point \( P\left( {s, t}\right) \) . What is \( \left| {s - t}\right| \) ?
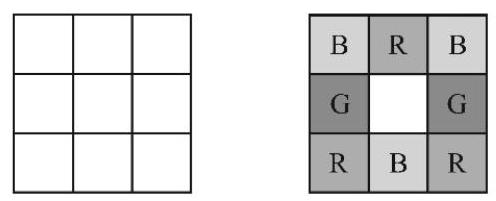
- Each square in a \( 3 \times 3 \) grid of squares is colored red, white, blue, or green so that every \( 2 \times 2 \) square contains one square of each color. One such coloring is shown on the right below. How many different colorings are possible?
- Let \( P\left( x\right) \) be the unique polynomial of minimal degree with the following properties:
- \( P\left( x\right) \) has leading coefficient 1,
- 2 is a root of \( P\left( {x - 2}\right) \) ,
- 3 is a root of \( P\left( {3x}\right) \) , and
- 4 is a root of \( {4P}\left( x\right) \) .
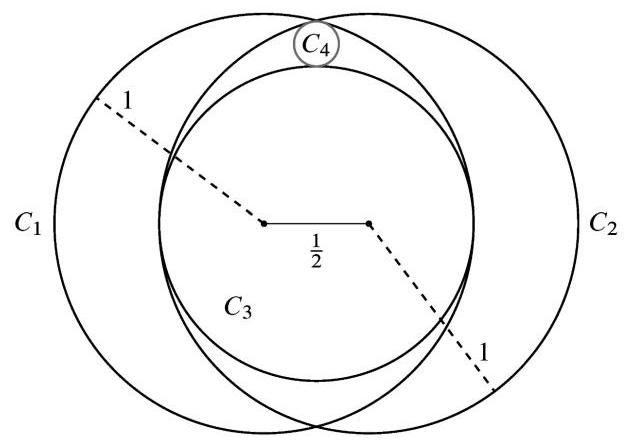
- Circles \( {C}_{1} \) and \( {C}_{2} \) each have radius 1, and the distance between their centers is \( \frac{1}{2} \) . Circle \( {C}_{3} \) is the largest circle internally tangent to both \( {C}_{1} \) and \( {C}_{2} \) . Circle \( {C}_{4} \) is internally tangent to both \( {C}_{1} \) and \( {C}_{2} \) and externally tangent to \( {C}_{3} \) . What is the radius of \( {C}_{4} \) ?
- If the positive integer \( c \) has positive integer divisors \( a \) and \( b \) with \( c = {ab} \) , then \( a \) and \( b \) are said to be complementary divisors of \( c \) . Suppose that \( N \) is a positive integer that has one complementary pair of divisors that differ by 20 and another pair of complementary divisors that differ by 23 . What is the sum of the digits of \( N \) ?
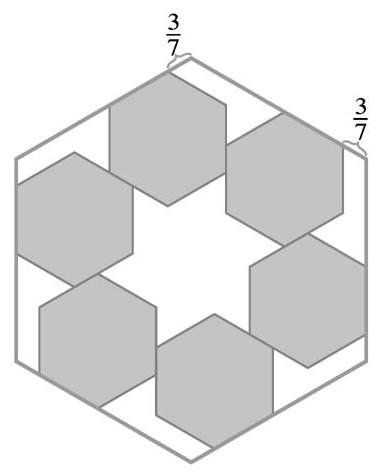
- Six regular hexagonal blocks of side length 1 unit are arranged inside a regular hexagonal frame. Each block lies along an inside edge of the frame and is aligned with two other blocks, as shown in the figure below. The distance from any corner of the frame to the nearest vertex of a block is \( \frac{3}{7} \) unit. What is the area of the region inside the frame not occupied by the blocks?
- If \( A \) and \( B \) are vertices of a polyhedron, define the distance \( d\left( {A, B}\right) \) to be the minimum number of edges of the polyhedron one must traverse in order to connect \( A \) and \( B \) . For example, if \( \overline{AB} \) is an edge of the polyhedron, then \( d\left( {A, B}\right) = 1 \) , but if \( \overline{AC} \) and \( \overline{CB} \) are edges and \( \overline{AB} \) is not an edge, then \( d\left( {A, B}\right) = 2 \) . Let \( Q, R \) , and \( S \) be randomly chosen distinct vertices of a regular icosahedron (regular polyhedron made up of 20 equilateral triangles). What is the probability that \( d\left( {Q, R}\right) > d\left( {R, S}\right) \) ?
\( A \) 城与 \( B \) 城相距 45 英里. Alicia 住在 \( A \) 城, Beth 住在 \( B \) 城. Alicia 以每小时 18 英里的速度骑自行车前往 \( B \) 城. Beth 同时出发,以每小时 12 英里的速度骑自行车前往 \( A \) 城. 问当他们相遇时,距离 \( A \) 城有多少英里?
(A) 20
(B) 24
(C) 25
(D) 26
(E) 27
一个大比萨饼的 \( \frac{1}{3} \) 与 \( 3\frac{1}{2} \) 杯橙片合在一起的重量与一个大比萨饼的 \( \frac{3}{4} \) 与 \( \frac{1}{2} \) 杯橙片合在一起的重量相同. 一杯橙片的重量是 \( \frac{1}{4} \) 磅. 问一个大比萨饼的重量是多少磅?
(A) \( 1\frac{4}{5} \)
(B) 2
(C) \( 2\frac{2}{5} \)
(D) 3
(E) \( 3\frac{3}{5} \)
2023 MAA AMC 10A
(A) 8
(B) 9
(C) 10
(D) 11
(E) 12
一个四边形的各边长均为整数,周长为 26 ,其中某一条边的长度为 4 . 问这个四边形的一条边最大可能的长度是多少?
(A) 9
(B) 10
(C) 11
(D) 12
(E) 13
(A) 14
(B) 15
(C) 16
(D) 17
(E) 18
2023 MAA AMC 10A
立方体的每个顶点处指定了一个整数. 每条边的值定义为它所接触的两个顶点处的数之和, 每个面的值定义为它的四条边的值之和. 立方体的值定义为它的六个面的值之和. 假设各顶点处指定的整数之和为 21. 问立方体的值是多少?
(A) 42
(B) 63
(C) 84
(D) 126
(E) 252
Janet 先后抛掷了标准的 6 面骰子 4 次, 并逐次记录她掷出数的总和. 问在某次抛掷后, 她掷出数的总和等于 3 的概率是多少?
(A) \( \frac{2}{9} \)
(B) \( \frac{49}{216} \)
(C) \( \frac{25}{108} \)
(D) \( \frac{17}{72} \)
(E) \( \frac{13}{54} \)
2023 MAA AMC 10A
面包师 Barb 为她的面包店开发了一种新的温标, 称为 Breadus 温标, 它是华氏温标的线性函数. 面包发酵的温度为 110 华氏度, 在 Breadus 温标中是 0 度. 面包烘烤的温度为 350 华氏度, 在 Breadus 温标中是 100 度. 当面包内部温度达到 200 华氏度时, 面包就烤好了. 问与此对应的 Breadus 温标是多少度?
(A) 33
(B) 34.5
(C) 36
(D) 37.5
(E) 39
电子显示器将当前日期显示为 8 位整数, 其中包括表示年份的 4 位数字, 后面跟着表示月份的 2 位数字,接下来是表示日子的 2 位数字. 例如, 今年美国的植树节显示为 20230428. 问 2023 年有多少个日期,使得每个数字在该日期的 8 位显示中都出现偶数次?
(A) 5
(B) 6
(C) 7
(D) 8
(E) 9
2023 MAA AMC 10A
Maureen 一直关注着她本学期各次测验成绩的平均分. 如果 Maureen 在下一次测验中获得 11 分, 那么她的平均分将增加 1 分. 如果她在接下来的三次测验中每次都获得 11 分, 那么她的平均分将增加 2 分. 问她目前的各次测验成绩的平均分是多少分?
(A) 4
(B) 5
(C) 6
(D) 7
(E) 8
如下图所示,面积为 2 的正方形内接于面积为 3 的正方形,并由此形成了四个全等的三角形. 问阴影直角三角形中较短的直角边与较长的直角边之比是多少?
(A) \( \frac{1}{5} \)
(B) \( \frac{1}{4} \)
(C) \( 2 - \sqrt{3} \)
(D) \( \sqrt{3} - \sqrt{2} \)
(E) \( \sqrt{2} - 1 \)
2023 MAA AMC 10A
满足以下性质的三位正整数 \( N \) 有多少个?
(A) 13
(B) 14
(C) 15
(D) 16
(E) 17
Abdul 和 Chiang 站在田地上, 相距 48 英尺. Bharat 站在同一块地上, 他在保持看 Abdul 与看 Chiang 的两条视线夹角为 \( {60}^{ \circ } \) 的情况下,离 Abdul 尽可能远. 问 Abdul 与 Bharat 之间距离英尺数的平方是多少?
(A) 1728
(B) 2601
(C) 3072
(D) 4608
(E) 6912
2023 MAA AMC 10A
从前 100 个正整数中随机选取一个数, 然后随机选取该数的一个正整数约数. 问所选的约数能被 11 整除的概率是多少?
(A) \( \frac{4}{100} \)
(B) \( \frac{9}{200} \)
(C) \( \frac{1}{20} \)
(D) \( \frac{11}{200} \)
(E) \( \frac{3}{50} \)
偶数个圆嵌套在一起,他们的半径从 1 开始,逐一增加 1 ,所有的圆有一个公共点. 从半径 2 的圆中在半径 1 的圆外的区域开始, 每隔一个区域, 将相邻两个圆之间的区域涂为阴影. 下面显示了一个有 8 个圆嵌套的例子. 为使得阴影部分的总面积至少为 2023π,最少需要多少个圆?

(A) 46
(B) 48
(C) 56
(D) 60
(E) 64
2023 MAA AMC 10A
在乒乓球锦标赛中,每位参赛者与其他参赛者恰好比赛一场. 尽管右手执拍的参赛者人数是左手执拍的参赛者人数的两倍,但左手执拍的参赛者获胜的场次比右手执拍的参赛者获胜的场次多 40%. (比赛没有平局,也没有参赛者既是右手执拍又是左手执拍.)问一共进行了多少场比赛?
(A) 15
(B) 36
(C) 45
(D) 48
(E) 66
在矩形 \( {ABCD} \) 中, \( {AB} = {30},{BC} = {28} \) . 点 \( P \) 和 \( Q \) 分别位于边 \( \overline{BC} \) 和 \( \overline{CD} \) 上, 使得 \( \bigtriangleup {ABP},\bigtriangleup {PCQ},\bigtriangleup {QDA} \) 的所有边的长度都是整数. 问 \( \bigtriangleup {APQ} \) 的周长是多少?
(A) 84
(B) 86
(C) 88
(D) 90
(E) 92
2023 MAA AMC 10A
如果一个凸多面体有 12 个面, 并且所有面都是彼此全等的菱形, 那么它称为 “菱形十二面体”. 如果在菱形十二面体的每个顶点处交汇的边的数量均为 3 或 4 . 问恰好有 3 条边交汇的顶点有多少个?
(A) 5
(B) 6
(C) 7
(D) 8
(E) 9
从 \( A\left( {1,2}\right) \) 到 \( B\left( {3,3}\right) \) 的线段可以通过以 \( P\left( {s, t}\right) \) 为中心的旋转,变换为从 \( {A}^{\prime }\left( {3,1}\right) \) 到 \( {B}^{\prime }\left( {4,3}\right) \) 的线段,将 \( A \) 送到 \( {A}^{\prime } \) ,将 \( B \) 送到 \( {B}^{\prime } \) . 问 \( \left| {s - t}\right| \) 是多少?
(A) \( \frac{1}{4} \)
(B) \( \frac{1}{2} \)
(C) \( \frac{2}{3} \)
(D) \( \frac{3}{4} \)
(E) 1
2023 MAA AMC 10A
\( 3 \times 3 \) 方格表的每个方格都涂为红色、白色、蓝色或绿色,使得每个 \( 2 \times 2 \) 正方形中包含每种颜色的方格各一个. 右下图显示了一种这样的涂色方法. 问共有多少种不同的涂色方法?
(A) 24
(B) 48
(C) 60
(D) 72
(E) 96
2023 MAA AMC 10A
-1 is a root of \( P\left( x\right) - 1 \) ,
The roots of \( P\left( x\right) \) are integers, with one exception. The root that is not an integer can be written as \( \frac{m}{n} \) , where \( m \) and \( n \) are relatively prime positive integers. What is \( m + n \) ?
令 \( P\left( x\right) \) 是唯一的具有以下性质并且次数最小的多项式:
\( \bullet P\left( x\right) \) 的首项系数为 1,
\( \bullet 1 \) 是 \( P\left( x\right) - 1 \) 的根,
-2 是 \( P\left( {x - 2}\right) \) 的根,
-3 是 \( P\left( {3x}\right) \) 的根,
\( \bullet 4 \) 是 \( {4P}\left( x\right) \) 的根.
\( P\left( x\right) \) 的根除去一个以外都是整数. 这个不是整数的根可以写作 \( \frac{m}{n} \) ,其中 \( m \) 和 \( n \) 是互质的正整数. 问 \( m + n \) 是多少?
(A) 41
(B) 43
(C) 45
(D) 47
(E) 49
2023 MAA AMC 10A
圆 \( {C}_{1} \) 和 \( {C}_{2} \) 的半径均为 1,圆心之间的距离为 \( \frac{1}{2} \) . 圆 \( {C}_{3} \) 是与 \( {C}_{1} \) 和 \( {C}_{2} \) 内切的最大圆. 圆 \( {C}_{4} \) 与 \( {C}_{1} \) 和 \( {C}_{2} \) 内切,并且与 \( {C}_{3} \) 外切. 问 \( {C}_{4} \) 的半径是多少?
(A) \( \frac{1}{14} \)
(B) \( \frac{1}{12} \)
(C) \( \frac{1}{10} \)
(D) \( \frac{3}{28} \)
(E) \( \frac{1}{9} \)
2023 MAA AMC 10A
如果正整数 \( c \) 有正整数约数 \( a \) 和 \( b \) ,满足 \( c = {ab} \) ,那么 \( a \) 和 \( b \) 被称为 \( c \) 的“配对约数”. 假设正整数 \( N \) 有一对相差为 20 的配对约数,和另一对相差为 23 的配对约数. 问 \( N \) 的各位数字之和是多少?
(A) 9
(B) 13
(C) 15
(D) 17
(E) 19
2023 MAA AMC 10A
在一个正六边形的框架内排列着六个边长为 1 个单位的正六边形木片. 如下图所示,每个木片都沿着框架的内部边缘摆放,并与其他两个木片边相贴合. 从框架的任意一角到木片的最近顶点的距离是 \( \frac{3}{7} \) 个单位. 问框架内未被木片占据的区域的面积是多少?
(A) \( \frac{{13}\sqrt{3}}{3} \)
(B) \( \frac{{216}\sqrt{3}}{49} \)
(C) \( \frac{9\sqrt{3}}{2} \)
(D) \( \frac{{14}\sqrt{3}}{3} \)
(E) \( \frac{{243}\sqrt{3}}{49} \)
2023 MAA AMC 10A
设 \( A \) 和 \( B \) 是多面体的顶点,“距离” \( d\left( {A, B}\right) \) 定义为由多面体的边来形成连接 \( A \) 与 \( B \) 的通路所需的最少边数. 例如,若 \( \overline{AB} \) 是多面体的边,则 \( d\left( {A, B}\right) = 1 \) , 但如果 \( \overline{AC} \) 和 \( \overline{CB} \) 是多面体的边,并且 \( \overline{AB} \) 不是,那么 \( d\left( {A, B}\right) = 2 \) . 令 \( Q \) , \( R, S \) 为随机选择的正二十面体 (由 20 个等边三角形组成的正多面体) 的不同顶点. 问 \( d\left( {Q, R}\right) > d\left( {R, S}\right) \) 的概率是多少?
(A) \( \frac{7}{22} \)
(B) \( \frac{1}{3} \)
(C) \( \frac{3}{8} \)
(D) \( \frac{5}{12} \)
(E) \( \frac{1}{2} \)
2023 MAA AMC 10A
Answers.
EAADE DBDED CBCBE BADED DDCCA